Módulo 1.4 – Bathymetry
Bathymetry (protótipo em teste)
(Metodologia para obter a batimetria derivada de satélite)
O conhecimento da batimetria é crucial na determinação de cenários associados a mudanças climáticas em zonas costeiras, ou seja, servem de condições de contorno na modelagem numérica, que necessita de batimetria atualizada para prever, por exemplo, cotas de inundação face à hidrodinâmica local (Alves et al., 2014, <https://doi.org/10.1016/j.marpolbul.2014.06.034>). A Batimetria Derivada de Satélite (BDS) é uma técnica útil para mapear a batimetria de águas rasas, caracterizar a área costeira e monitorar as mudanças do fundo marinho que podem ter ocorrido desde o último levantamento batimétrico realizado (Lyzenga, 1978, <https://opg.optica.org/ao/abstract.cfm?URI=ao-17-3-379>).
A BDS explora o princípio físico de que os diferentes comprimentos de onda do espectro de luz são atenuados pela água em graus variados, e com isso, é possível fazer estimativas no campo da profundidade devido à inversão óptica da refletância do fundo (Philpot, 1989, <https://opg.optica.org/ao/abstract.cfm?URI=ao-28-8-1569>). Esse procedimento tem se mostrado eficaz, principalmente na utilização das imagens de satélites multiespectrais e apresenta vantagens como a cobertura de extensa área e a repetitividade (Nordman et al., 1990). A batimetria sublitoral pode ser obtida através do algoritmo desenvolvido por Stumpf et al. (2003, <https://doi.org/10.4319/lo.2003.48.1_part_2.0547>), que estima a profundidade através da razão do logaritmo natural entre a reflectância de duas bandas, assumindo que ambas as bandas são afetadas igualmente pela atmosfera, coluna d’água e contribuição da refletância do fundo marinho (Eq. 1).
𝑅𝐵 = (ln(𝑛𝑅𝑤(𝜆𝑖) ln(𝑛𝑅𝑤(𝜆𝑗)) [Eq. 1]
Em que RB é o modelo de razão de bandas proposto por Stumpf et al. (2003) ainda sem referência vertical, n é uma constante para garantir que a razão permaneça positiva em todos os valores, Rw(𝜆i) é a refletância da superfície da banda i e Rw(𝜆j) é a refletância da superfície da banda j. A relação entre modelo RB e a batimetria local é tipicamente descrito através de regressão polinomial de segundo grau (Eq. 2) assim como utilizado por Vilar et al. (2018, <https://www.researchgate.net/publication/331135587>):
𝑍𝑠𝑎𝑡= m2 (𝑅𝐵)² + m1(𝑅𝐵) + m0 [Eq. 2]
Em que, Zsat é a profundidade estimada pelo satélite, RB é o resultado do algoritmo proveniente da Equação 1, m1 e m2 são os coeficientes de ajuste da curva que dimensionam a profundidade de referência e m0 é o offset de ajuste da maré. Segundo Filippi (2020, <https://repositorio.ufsc.br/handle/123456789/209992>) a melhor razão de bandas para a estimativa da batimetria na Baía da Babitonga (SC, Brasil) pode ser descrita pelo algoritmo.
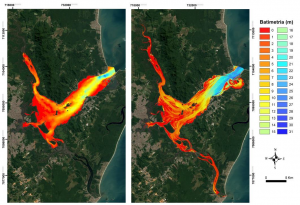
Figura 1. Exemplo da comparação entre a batimetria medida por eco-sonda de feixe simples (in situ) e batimetria derivada por satélite (BDS) com imagem Sentinel 2 (Copernicus) na zona estuarina da baía da Babitonga (Santa Catarina, Brasil) (Fonte: Fillipi et al., 2020).
Para a criação do módulo de batimetria derivada de satélite [Bathymetry] as Equações [1 e 2] serão implementadas em código JavaScript (linguagem de programação utilizada pela plataforma GEE). Complementarmente, o módulo [Bathymetry] possuirá algoritmos para seleção dos pixels adequados ao processamento de inversão ótica (remoção de nuvens, sombras, áreas com elevado sedimento em suspensão, etc.) assim como metodologias para otimização do intervalo temporal de imagens a serem utilizadas (e.g., imagens medianas de um conjunto de imagens) e diferentes modelos matemáticos para a geração do modelo de inversão (etapa final da criação de um modelo de inversão ótica).






